6927. В треугольнике ABC
точка M
— середина BC
, P
— точка пересечения касательных в точках B
и C
к описанной окружности, N
— середина отрезка MP
. Отрезок AN
пересекает описанную окружность в точке Q
. Докажите, что \angle PMQ=\angle MAQ
.
Указание. Докажите, что MN
— касательная к окружности, описанной вокруг треугольника AMQ
.
Решение. Достаточно доказать, что MN
— касательная к окружности, описанной вокруг треугольника AMQ
(см. задачу 87), т. е. равенство NM^{2}=NQ\cdot NA
(см. задачу 4776).
Пусть O
— центр окружности радиуса R
, описанной вокруг треугольника ABC
. Обозначим через \deg_{\omega}N
степень точки N
относительно описанной окружности \omega
радиуса R
треугольника ABC
. Тогда (см. задачи 2635, 2636)
\deg_{\omega}N=NO^{2}-R^{2}=(NM+OM)^{2}-R^{2}=
=NM^{2}+2NM\cdot OM+OM^{2}-R^{2}=NM^{2}+PM\cdot OM+OM^{2}-R^{2}.
Поскольку PB
— касательная к окружности, а M
— середина хорды BC
, треугольник BOP
— прямоугольный, а BM
— его высота, опущенная на гипотенузу. Значит, PM\cdot OM=BM^{2}
. Тогда
\deg_{\omega}N=NM^{2}+BM^{2}+OM^{2}-R^{2}=NM^{2}+OB^{2}-R^{2}=NM^{2}.
С другой стороны, степень точки N
относительно окружности \omega
равна NQ\cdot NA
, т. е. NM^{2}=NQ\cdot NA
. Что и требовалось доказать.
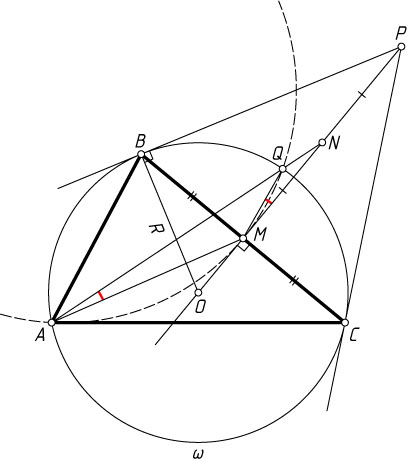
Автор: Гаркавый А. А.
Источник: Олимпиада по геометрии им. И. Ф. Шарыгина. — 2015, 10-11 класс
Источник: Московская устная олимпиада по геометрии. — 2015, № 10, 10-11 классы
