9595. На ребре SD
правильной четырёхугольной пирамиды SABCD
с основанием ABCD
отмечена точка M
, причём SM:MD=1:4
. Точки P
и Q
— середины рёбер BC
и AD
соответственно.
а) Докажите, что сечение пирамиды плоскостью MPQ
является равнобедренной трапецией.
б) Найдите отношение объёмов многогранников, на которые плоскость MPQ
разбивает пирамиду.
Ответ. 11:14
.
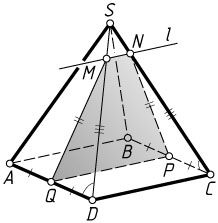
Решение. а) Прямая PQ
параллельна плоскости CSD
, так как эта прямая параллельна прямой CD
, лежащей в плоскости CSD
(см. задачу 8002). Плоскость PQM
проходит через прямую PQ
, параллельную плоскости CSD
, и пересекает эту плоскость по прямой l
, проходящей через точку M
, значит, прямая l
параллельна прямой PQ
(см. задачу 8004). Пусть прямая l
пересекает ребро SC
в точке N
. Тогда PQMN
— трапеция, так как PQ\parallel MN
и MN\ne PQ
, а так как из равенства треугольников PCN
и QDM
следует, что PN=QM
, то эта трапеция равнобедренная.
б)
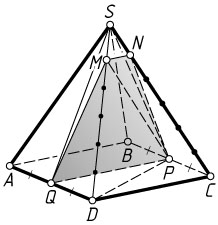
Первый способ. Пусть объём данной пирамиды равен V
. Тогда объём четырёхугольной пирамиды SCPQD
, основание которой — прямоугольник CDQP
, равен \frac{1}{2}V
. Плоскость PDQ
разбивает её на две треугольные пирамиды, объём каждой из которых равен \frac{1}{4}V
.
Плоскость PMN
отсекает от треугольной пирамиды SCDP
треугольную пирамиду SPMN
, объём которой равен
\frac{SM}{SD}\cdot\frac{SN}{SC}\cdot\frac{SP}{SP}\cdot\frac{1}{4}V=\frac{1}{5}\cdot\frac{1}{5}\cdot1\cdot\frac{1}{4}V=\frac{1}{100}V
(см. задачу 7244). Эта же плоскость отсекает от треугольной пирамиды SPDQ
треугольную пирамиду SPMQ
, объём которой равен
\frac{SM}{SD}\cdot\frac{SQ}{SQ}\cdot\frac{SP}{SP}\cdot\frac{1}{4}V=\frac{1}{5}\cdot1\cdot1\cdot\frac{1}{4}V=\frac{1}{20}V.
Значит, плоскость PMN
отсекает от четырёхугольной пирамиды SCPQD
четырёхугольную пирамиду SMNPQ
, объём которой равен
\frac{1}{100}V+\frac{1}{20}V=\frac{3}{50}V.
Тогда объём оставшейся части четырёхугольной пирамиды SCPQD
равен
\frac{1}{2}V-\frac{3}{50}V=\frac{11}{25}V.
Таким образом, плоскость PMN
разбивает данную пирамиду SABCD
на два многогранника с объёмами \frac{11}{25}V
и V-\frac{11}{25}V=\frac{14}{25}V
. Следовательно, отношение объёмов этих многогранников равно \frac{11}{14}
.
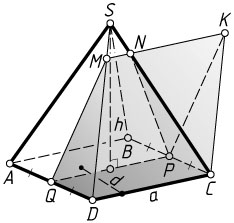
Второй способ. Достроим трапецию PQMN
до параллелограмма PQMK
. Тогда DMQCKP
— треугольная призма с основаниями MDQ
и CKP
.
Пусть сторона основания данной пирамиды равна a
, высота равна h
, а расстояние от прямой CD
до секущей плоскости равно d
. Тогда расстояние от бокового ребра MK
призмы DMQCKP
до её грани CDQP
равно \frac{4}{5}h
, а площадь этой грани равна \frac{a^{2}}{2}
. Тогда объём призмы равен
\frac{1}{2}\cdot\frac{a^{2}}{2}\cdot\frac{4}{5}h=\frac{a^{2}h}{5}=\frac{1}{3}a^{2}h\cdot\frac{3}{5}=\frac{3}{5}V
(см. задачу 7237), где V
— объём данной пирамиды SABCD
.
Пусть S
— площадь грани PKMQ
призмы DMQCKP
. Тогда площадь грани PKN
треугольной пирамиды KPCN
равна \frac{2}{5}S
, а объём этой пирамиды равен
\frac{1}{3}\cdot\frac{2}{5}S\cdot d=\frac{2}{15}Sd=\frac{4}{15}\cdot\frac{1}{2}Sd=\frac{4}{15}\cdot\frac{3}{5}V=\frac{4}{25}V.
Объём части пирамиды SABCD
, содержащей точку C
, равен разности объёмов призмы DMQCKP
и пирамиды KPCN
, т. е.
\frac{3}{5}V-\frac{4}{25}V=\frac{11}{25}V,
а объём остальной части равен V-\frac{11}{25}V=\frac{14}{25}V
. Следовательно, искомое отношение объёмов равно \frac{11}{14}
.
Источник: ЕГЭ. — 2017


