1227. Сумма углов при одном из оснований трапеции равна 90^{\circ}
. Докажите, что отрезок, соединяющий середины оснований трапеции, равен полуразности оснований.
Указание. Через середину меньшего основания проведите прямые, параллельные боковым сторонам трапеции (или воспользуйтесь утверждениями задач 1234 и 1226).
Решение. Первый способ. Пусть M
и N
— середины оснований соответственно BC
и AD
трапеции ABCD
, P
и Q
— середины диагоналей AC
и BD
соответственно, а прямые AB
и CD
пересекаются в точке F
. По условию \angle A+\angle D=90^{\circ}
, поэтому
\angle AFD=180^{\circ}-(\angle A+\angle D)=180^{\circ}-90^{\circ}=90^{\circ}.
Следовательно, AB\perp CD
.
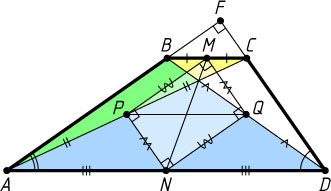
Предположим, что AD\gt BC
. Отрезки PM
и QN
— средние линии треугольников ABC
и ABD
, поэтому PM=\frac{1}{2}AB
и QN=\frac{1}{2}AB
, значит, PM=QN
. Аналогично, QM=PN
, поэтому PMQN
— параллелограмм. Кроме того, PM\parallel AB
и QM\parallel CD
, а так как AB\perp CD
, то PM\perp QM
, значит, PMQN
— прямоугольник. Его диагонали MN
и PQ
равны, следовательно, MN=PQ=\frac{AD-BC}{2}
(см. задачу 1226).
Второй способ. Пусть M
и N
— середины оснований BC
и AD
трапеции ABCD
(AD=a
, BC=b
, a\gt b
) и \angle A+\angle D=90^{\circ}
.
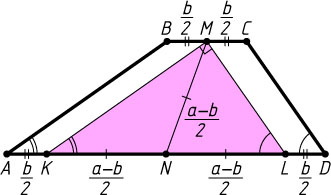
Через точку M
проведём прямые, параллельные AB
и CD
. Пусть K
и L
— точки их пересечения с основанием AD
. Тогда
\angle MKL+\angle MLK=\angle A+\angle D=90^{\circ}.
Поэтому \angle KML=90^{\circ}
. Кроме того,
NK=AN-AK=AN-BM=DN-CM=DN-DL=NL.
Значит, MN
— медиана прямоугольного треугольника KML
, проведённая из вершины прямого угла. Поэтому MN=\frac{1}{2}KL
(см. задачу 1109), а так как
KL=AD-AK-LD=a-\frac{1}{2}b-\frac{1}{2}b=a-b,
то
MN=\frac{1}{2}KL=\frac{a-b}{2}.
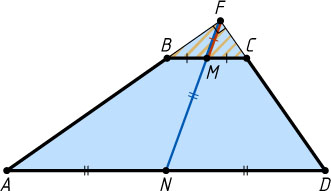
Третий способ. Пусть F
— точка пересечения прямых AB
и CD
, содержащих боковые стороны трапеции ABCD
. Точка F
и середины M
и N
оснований BC
и AD
лежат на одной прямой (см. задачу 1513). Отрезки FN
и FM
— медианы прямоугольных треугольников AFD
и BFC
, следовательно (см. задачу 1109),
MN=FN-FM=\frac{1}{2}AD-\frac{1}{2}BC=\frac{AD-BC}{2}.
Примечание. Верно и обратное, если продолжения двух противоположных сторон выпуклого четырёхугольника пересекаются под прямым углом, а отрезок, соединяющий середины двух других сторон, равен их полуразности, то четырёхугольник — трапеция (см. задачу 12505).
Источник: Вступительный экзамен в МФТИ. — 1958, билет 9, № 1
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 58-9-1, с. 64
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 439, с. 113
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 5.23, с. 104


