13454. Высоты BB_{1}
и CC_{1}
остроугольного треугольника ABC
пересекаются в точке H
; \angle A=60^{\circ}
, AB\lt AC
; медиана AM
пересекает описанную окружность треугольника ABC
вторично в точке K
; L
— середина дуги BC
описанной окружности, не содержащей точку A
; прямые B_{1}C_{1}
и BC
пересекаются в точке E
. Докажите, что \angle EHL=\angle ABK
.
Решение. Лемма 1. Прямые MH
и AE
перпендикулярны.
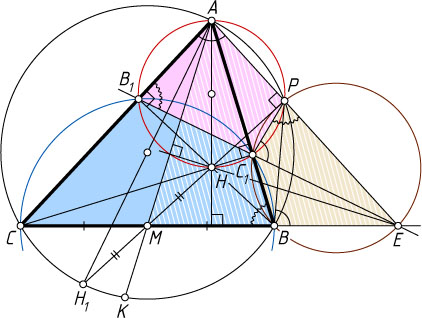
Доказательство. Пусть H_{1}
— точка, симметричная ортоцентру H
относительно точки M
(рис. 1). Тогда она лежит на окружности, описанной около треугольника ABC
и диаметрально противоположна точке A
(см. задачу 6300). Следовательно, проекция P
точки A
на прямую MH
— точка пересечения двух окружностей с диаметрами AH
и AH_{1}
, т. е. описанных окружностей треугольников AB_{1}C_{1}
и ABC
.
Осталось доказать, что точки A
, P
и E
лежат на одной прямой. Это можно сделать, например, так: четырёхугольники PAB_{1}C_{1}
и PACB
вписанные, поэтому
\angle PC_{1}E=\angle PAC=\angle PBE,
значит, четырёхугольник PC_{1}BE
тоже вписанный; кроме того,
\angle APC_{1}=180^{\circ}-\angle AB_{1}C_{1}=180^{\circ}-\angle ABC=180^{\circ}-\angle EPC_{1},
так как четырёхугольник B_{1}C_{1}BC
тоже вписанный (см. задачу 12). Следовательно, точки A
, P
и E
лежат на одной прямой. Отсюда следует доказательство леммы.
Лемма 2. Прямые EH
и AK
перпендикулярны.
Доказательство. Рассмотрим треугольник MAE
. Из леммы 1 следует, что H
— его ортоцентр. Тогда EH
и AM
перпендикулярны, что и требовалось. (См. также задачу 6146.)
Лемма 3. Если \angle A=60^{\circ}
, то прямые LH
и B_{1}C_{1}
перпендикулярны.
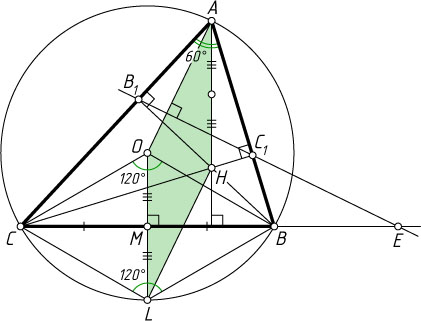
Доказательство. Пусть O
— центр описанной окружности треугольника ABC
(рис. 2). Поскольку \angle A=60^{\circ}
, то
\angle BOC=120^{\circ}=\angle BLC,
поэтому точки O
и L
симметричны относительно прямой BC
, а так как AH\parallel OL
и AH=2OM=OL
(см. задачу 1257), то AOLH
— параллелограмм. Значит, LH\parallel AO
. По теореме Нагеля (см. задачу 480) прямые AO
и B_{1}C_{1}
перпендикулярны. Отсюда следует доказательство леммы.
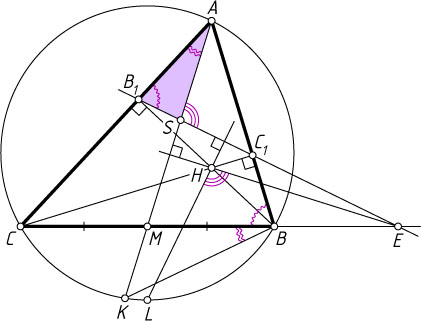
Вернёмся к нашей задаче. Пусть S
— точка пересечения прямых AK
и B_{1}C_{1}
(рис. 3). Из лемм 2 и 3 следует, что \angle EHL=\angle ASE
, как тупые углы с соответственно перпендикулярными сторонами. Кроме того,
\angle ABK=\angle CBK+\angle ABC=\angle CAK+\angle AB_{1}C_{1}=\angle ASE
(так как ASE
— внешний угол треугольника ASB_{1}
). Отсюда следует утверждение задачи.
Автор: Аполонская К. О.
Источник: Московская устная олимпиада по геометрии. — 2023, XX, задача 5, 8-9 класс


