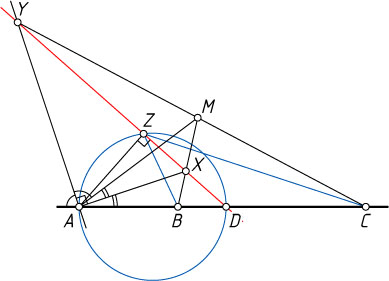
13783. Пусть A
, B
и C
— различные точки, лежащие на одной прямой, а M
— произвольная точка, не лежащая на этой прямой. Биссектриса угла MAB
пересекает прямую MB
в точке X
. Прямая, проведённая через точку A
перпендикулярно AX
, пересекает прямую MC
в точке Y
.
а) Докажите, что прямая XY
проходит через фиксированную точку D
.
б) Пусть Z
— проекция точки A
на прямую XY
. Докажите, что \angle BZD=\angle CZD
.
Решение. Рассмотрим случай, изображённый на рисунке.
а) Пусть прямая XY
пересекает прямую AC
в точке D
. Поскольку AX
— биссектриса треугольника ABM
, а AY\perp AX
, то AY
— биссектриса внешнего угла при вершине A
этого треугольника (см. задачу 937). Тогда (см. задачи 1645 и 1509)
\frac{YM}{YC}=\frac{AM}{AC},~\frac{XM}{XB}=\frac{AM}{AB}.
По теореме Менелая для треугольника BCM
и прямой XY
получаем
\frac{YM}{YC}\cdot\frac{DC}{DB}\cdot\frac{XB}{XM}=1,
откуда
\frac{DC}{DB}=\frac{YC}{YM}\cdot\frac{XM}{XB}=\frac{AC}{AM}\cdot\frac{AM}{AB}=\frac{AC}{AB}.
Значит, положение точки D
на прямой AC
фиксировано. Отсюда следует утверждение а).
б) Выше доказано, что \frac{DC}{DB}=\frac{AC}{AB}
. Обозначим это отношение через k
. Тогда точки A
и D
лежат на окружности Аполлония отрезка BC
и отношения k
(см. задачу 2444), а так как отрезок AD
виден из точки Z
под прямым углом, то Z
лежит на этой окружности (AD
— диаметр). Значит, \frac{ZC}{ZB}=k=\frac{DC}{DB}
. Следовательно, ZD
— биссектриса угла BZC
(см. задачу 1510).
Источник: Журнал «Crux Mathematicorum». — 2006, № 4, задача 3036 (2005, 175, 178), с. 244
