1434. Отрезки, соединяющие основания высот остроугольного треугольника, равны 8, 15 и 17. Найдите площадь треугольника.
Ответ. 340.
Указание. 1. Если R
— радиус описанной окружности треугольника ABC
, то
S_{\triangle ABC}=2R^{2}\sin A\sin B\sin C.
Точка, симметричная ортоцентру треугольника относительно прямой, содержащей сторону треугольника, лежит на описанной окружности.
2. См. задачи 480 и 3018.
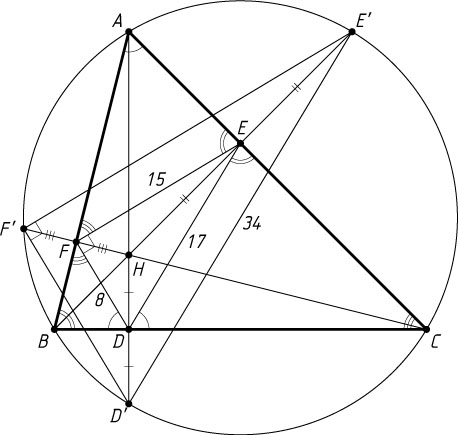
Решение. Первый способ. Пусть AD
, BE
и CF
— высоты остроугольного треугольника ABC
; DF=8
, EF=15
, DE=17
. Поскольку 8^{2}+15^{2}=17^{2}
, то треугольник DEF
— прямоугольный, \angle DFE=90^{\circ}
.
Обозначим через \alpha
, \beta
и \gamma
углы соответственно A
, B
и C
треугольника ABC
. Поскольку сторона AC
видна из точек F
и D
под прямым углом, эти точки лежат на окружности с диаметром AC
, значит,
\angle BDF=180^{\circ}-\angle CDF=\angle CAF=\alpha.
Аналогично докажем, что
\angle CDE=\alpha,~\angle CED=\beta,~\angle AEF=\beta,~\angle AFE=\gamma,~\angle BFD=\gamma,
Пусть R
— радиус описанной окружности треугольника ABC
. Тогда
S_{\triangle ABC}=2R^{2}\sin\alpha\sin\beta\sin\gamma
(см. задачу 4020).
Для того, чтобы найти R
, продолжим высоты AD
, BE
и CF
до пересечения с описанной окружностью в точках D'
, E'
и F'
соответственно. Если H
— точка пересечения высот треугольника ABC
, то точки D
, E
и F
— середины отрезков HD'
, HE'
и HF'
(см. задачу 4785). Поэтому EF
, DE
и DF
— средние линии треугольников E'HF'
, D'HE'
и D'HF'
. Значит, треугольник D'E'F'
подобен треугольнику DEF
с коэффициентом 2. Следовательно, треугольник D'E'F'
— прямоугольный, а радиус R
его описанной окружности равен половине гипотенузы E'D'
, т. е. 17.
Поскольку
\angle EDF=180^{\circ}-\angle BDF-\angle CDE=180^{\circ}-2\alpha~\mbox{и}~\cos\angle EDF=\frac{DF}{DE}=\frac{8}{17},
то
\frac{8}{17}=\cos\angle EDF=\cos(180^{\circ}-2\alpha)=-\cos2\alpha,
\sin\alpha=\sqrt{\frac{1-\cos2\alpha}{2}}=\sqrt{\frac{1+\frac{8}{17}}{2}}=\frac{5}{\sqrt{34}}.
Аналогично находим, что
\sin\beta=\frac{4}{\sqrt{17}},~\sin\gamma=\sin45^{\circ}=\frac{1}{\sqrt{2}}.
Следовательно,
S_{\triangle ABC}=2R^{2}\sin\alpha\sin\beta\sin\gamma=2\cdot17^{2}\cdot\frac{5}{\sqrt{34}}\cdot\frac{4}{\sqrt{17}}\cdot\frac{1}{\sqrt{2}}=340.
Второй способ. Пусть O
— центр описанной окружности треугольника ABC
, R
— её радиус. Пусть уже найдено, что R=17
.
Поскольку OA\perp EF
, OB\perp DF
и OC\perp DE
(см. задачу 480), диагонали четырёхугольников AFOE
, BDOF
и CDOE
перпендикулярны, следовательно (см. задачу 3018),
S_{\triangle ABC}=S_{AFOE}+S_{BDOF}+S_{CDOE}=\frac{1}{2}OA\cdot EF+\frac{1}{2}OB\cdot DF+\frac{1}{2}OC\cdot DE=
=\frac{1}{2}R(EF+DF+DE)=\frac{1}{2}\cdot17(15+8+17)=340.
Примечание. Если радиус описанной окружности найден, то можно применить готовую формулу для площади треугольника S=Rq
(см. примечание к задаче 4305), где R
— радиус описанной окружности треугольника, а q
— полупериметр его ортотреугольника.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1993, вариант 1, № 6
Источник: Журнал «Математика в школе». — 1994, № 1, с. 50
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 15.18, с. 123
