16441. Постройте прямоугольный треугольник по гипотенузе и лежащей на ней точке, являющейся вершиной вписанного в треугольник квадрата.
Решение. Рассмотрим случай, когда сторона вписанного в треугольник квадрата лежит на гипотенузе.
Пусть сторона PQ
квадрата PQMN
лежит на гипотенузе AB
треугольника ABC
, причём точка P
лежит между B
и Q
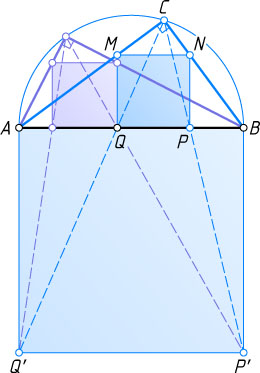
(рис. 1). Тогда при гомотетии с центром в вершине C
прямого угла треугольника ABC
, переводящей вершину M
в точку A
, точка N
переходит в B
, а квадрат PQMN
— в квадрат P'Q'AB
.
Отсюда вытекает следующий способ построения. На данном отрезке AB
строим квадрат P'Q'AB
, а по другую сторону от прямой AB
— полуокружность с диаметром AB
. Тогда луч Q'Q
пересекает полуокружность в вершине C
прямого угла искомого прямоугольного треугольника. Аналогично, предполагая, что точка P
лежит между Q
и A
, получим второе решение.
Рассмотрим случай, когда на гипотенузе AB
лежит единственная вершина Q
квадрата PQMC
, вписанного в треугольник ABC
.
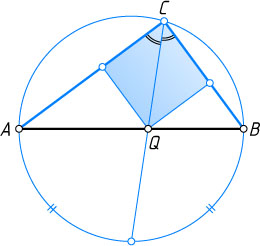
Первый способ. Заметим, что Q
— основание биссектрисы треугольника ABC
, проведённой из вершины прямого угла (рис. 2). Отсюда вытекает следующее построение.
На данном отрезке AB
строим как на диаметре окружность. Через середину одной из полуокружностей и данную точку Q
проводим прямую. Точка её пересечения со второй полуокружностью есть вершина C
искомого треугольника ABC
.
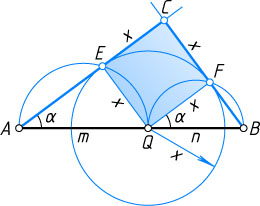
Второй способ. Пусть вершина Q
квадрата CFQE
со стороной x
лежит на гипотенузе AB
треугольника ABC
, а вершины E
и F
— на катетах AC
и BC
соответственно (рис. 3). Обозначим AQ=m
, BQ=n
, \angle A=\alpha
. Тогда
\sin\alpha=\frac{x}{m},~\cos\alpha=\frac{x}{n},
а так как
\left(\frac{x}{m}\right)^{2}+\left(\frac{x}{n}\right)^{2}=\sin^{2}\alpha+\cos^{2}\alpha=1,
то x=\frac{mn}{\sqrt{m^{2}+n^{2}}}
.
Можно по-другому. Повернём треугольник QFB
на 90^{\circ}
, чтобы точка F
совпала с E
. Получим прямоугольный треугольник с катетами m
, n
и высотой x=\frac{mn}{\sqrt{m^{2}+n^{2}}}
, опущенной из вершины прямого угла.
Отсюда вытекает следующее построение. По данным отрезкам AQ
и BQ
строим отрезок \sqrt{AQ^{2}+BQ^{2}}
(см. задачу 1966). Затем строим отрезок x=\frac{AQ\cdot BQ}{\sqrt{AQ^{2}+BQ^{2}}}
(см. задачу 2608). На отрезках AQ
и BQ
как на диаметрах строим полуокружности, а также окружность с центром Q
радиуса x
, пересекающую две уже построенные полуокружности в точках E
и F
соответственно. Наконец, проводим прямые AE
и BF
. Они пересекаются в точке C
— вершине прямого угла искомого прямоугольного треугольника ABC
.
Третий способ. По свойству биссектрисы треугольника \frac{CA}{CB}=\frac{QA}{QB}
(см. задачу 1509), поэтому точка C
лежит на окружности Аполлония данного отрезка AB
и данного отношения \frac{AQ}{BQ}
(см. задачу 2444). Следовательно, искомая вершина C
— точка пересечения этой окружности Аполлония (см. задачу 1826) и полуокружности с диаметром AB
.
Источник: Журнал «Mathematics Magazine». — 1954, том 28, № 2, задача 196, с. 108


