3257. Расстояния от центра описанной окружности остроугольного треугольника до его сторон равны d_{a}
, d_{b}
и d_{c}
соответственно, R
и r
— радиусы соответственно описанной и вписанной окружностей. Докажите, что d_{a}+d_{b}+d_{c}=R+r
(формула Карно).
Указание. 1. Пусть A_{1}
, B_{1}
и C_{1}
— середины сторон соответственно BC
, AC
и AB
треугольника ABC
. Примените теорему Птолемея (см. задачу 130) к вписанным четырёхугольникам AB_{1}OC_{1}
, BC_{1}OA_{1}
и CA_{1}OB_{1}
.
2. Примените равенство
\cos\alpha+\cos\beta+\cos\gamma=\frac{R+r}{R}
(см. задачу 3238).
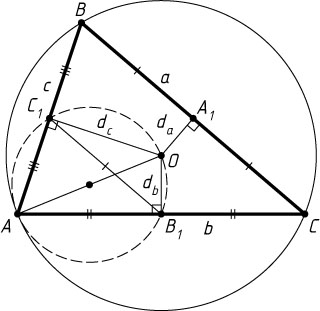
Решение. Первый способ. Пусть BC=a
, AC=b
, AB=c
— длины сторон треугольника, O
— центр описанной окружности, S
— площадь треугольника, A_{1}
, B_{1}
и C_{1}
— середины сторон BC
, AC
и AB
соответственно, OA_{1}=d_{a}
, OB_{1}=d_{b}
и OC_{1}=d_{c}
.
Из точек B_{1}
и C_{1}
отрезок OA
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OA
. Применив теорему Птолемея к вписанному четырёхугольнику AB_{1}OC_{1}
(см. задачу 130), получим, что
AB_{1}\cdot OC_{1}+AC_{1}\cdot OB_{1}=B_{1}C_{1}\cdot OA,
а так как B_{1}C_{1}
— средняя линия треугольника ABC
, то B_{1}C_{1}=\frac{a}{2}
. Поэтому
\frac{b}{2}\cdot d_{c}+\frac{c}{2}\cdot d_{b}=\frac{a}{2}\cdot R,~bd_{c}+cd_{b}=aR.
Аналогично,
cd_{a}+ad_{c}=bR,~ad_{b}+bd_{a}=cR.
Кроме того,
ad_{a}+bd_{b}+cd_{c}=2S=(a+b+c)r.
Сложив эти четыре равенства, получим, что
(bd_{c}+cd_{b})+(cd_{a}+ad_{c})+(ad_{b}+bd_{a})+(ad_{a}+bd_{b}+cd_{c})=
=aR+bR+cR+(a+b+c)r,
или
(a+b+c)d_{a}+(a+b+c)d_{b}+(a+b+c)d_{c}=(a+b+c)(R+r).
Следовательно, d_{a}+d_{b}+d_{c}=R+r
.
Второй способ. Из равенства
\cos\alpha+\cos\beta+\cos\gamma=\frac{R+r}{R}
(см. задачу 3238) следует, что
R\cos\alpha+R\cos\beta+R\cos\gamma=R+r,
а так как R\cos\alpha=d_{a}
, R\cos\beta=d_{b}
, R\cos\gamma=d_{c}
, то d_{a}+d_{b}+d_{c}=R+r
.
Третий способ. Пусть K_{a}
— точка пересечения биссектрисы угла BAC
с описанной окружностью треугольника ABC
, I_{a}
— центр вневписанной окружности, касающейся стороны BC
, P
и Q
— точки касания соответственно вписанной и указанной вневписанной окружностей со стороной BC
, r
и r_{a}
— их радиусы. Аналогично определим точки K_{b}
и K_{c}
, I_{b}
и I_{c}
, а также числа r_{b}
и r_{c}
.
Поскольку AP=CQ
(см. задачу 4805), середина A_{1}
стороны BC
совпадает с серединой диагонали PQ
трапеции PIQI_{a}
, а по теореме Мансиона (см. задачу 57) точка K_{a}
— середина диагонали II_{a}
этой трапеции. Значит,
A_{1}K_{a}=\frac{I_{a}Q-IP}{2}=\frac{r_{a}-r}{2}
(см. задачу 1226), а
R=OK_{a}=OA_{1}+A_{1}K_{a}=OA_{1}+\frac{r_{a}-r}{2}.
Аналогично,
R=OB_{1}+B_{1}K_{b}=OB_{1}+\frac{r_{b}-r}{2},~R=OC_{1}+C_{1}K_{c}=OC_{1}+\frac{r_{c}-r}{2}.
Сложив эти три равенства и учитывая что r_{a}+r_{b}+r_{c}=4R+r
(см. задачу 3240), получим, что
3R=OA_{1}+OB_{1}+OC_{1}+\frac{r_{a}+r_{b}+r_{c}-3r}{2}=
=OA_{1}+OB_{1}+OC_{1}+\frac{4R+r-3r}{2}=OA_{1}+OB_{1}+OC_{1}+2R-r,
откуда
d_{a}+d_{b}+d_{c}=OA_{1}+OB_{1}+OC_{1}=R+r.
Примечание. Если треугольник тупоугольный с тупым углом при вершине, противолежащей стороне a
, то d_{b}+d_{c}-d_{a}=R+r
. Тогда формулу Карно для произвольного треугольника ABC
можно записать в виде
R\cos\alpha+R\cos\beta+R\cos\gamma=R+r,
где \alpha
, \beta
и \cos\gamma
— углы треугольника ABC
.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — № 16, с. 24
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 175, с. 48
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 92, с. 172; № 64, с. 187
Источник: Вступительный экзамен в МФТИ. — 1958, билет 24, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 58-24-4, с. 69
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 6.37, с. 154
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.40, с. 155
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 30
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 226, с. 36
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 5.40, с. 46
