3495. Пусть A'
, B'
, C'
— проекции центра вписанной окружности треугольника ABC
на серединные перпендикуляры к сторонам BC
, AC
, AB
соответственно. Докажите, что прямые AA'
, BB'
, CC'
пересекаются в одной точке.
Указание. Прямые AA'
, BB'
, CC'
пересекают стороны треугольника в точках их касания с вневписанными окружностями треугольника.
Решение. Первый способ. Докажем, что прямые AA'
, BB'
, CC'
пересекают стороны треугольника в точках касания этих сторон с вневписанными окружностями. Отсюда будет следовать, что эти прямые пересекаются в одной точке — точке Нагеля (см. задачу 4284).
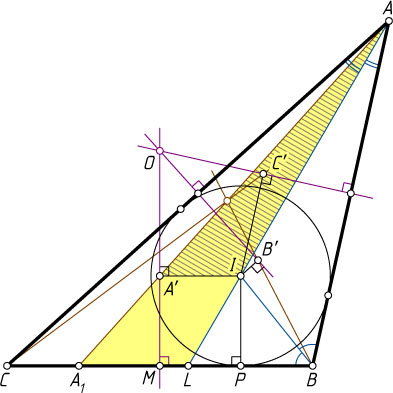
Пусть прямая AA'
пересекает сторону BC
в точке A_{1}
(рис. 1), I
— центр вписанной окружности треугольника ABC
, P
— точка касания этой окружности со стороной BC
, M
— середина BC
, AL
— биссектриса треугольника ABC
. Обозначим BC=a
, AC=b
, AB=c
, \frac{a+b+c}{2}=p
. Для определённости будем считать, что b\gt c
(для равнобедренного треугольника утверждение очевидно).
Тогда (см. задачи 219 и 2906)
BP=p-b=\frac{a+c-b}{2},~BL=\frac{ac}{b+c},
IA'=PM=BM-BP=\frac{a}{2}-\frac{a+c-b}{2}=\frac{b-c}{2},
PL=BL-BP=\frac{ac}{b+c}-\frac{a+c-b}{2}=
=\frac{2ac-(b+c)(a+c-b)}{2(b+c)}=\frac{(b-c)(b+c-a)}{2(b+c)},
а так как BI
— биссектриса треугольника ABL
, то
\frac{AI}{IL}=\frac{AB}{BL}=\frac{c}{\frac{ac}{b+c}}=\frac{b+c}{a}.
Из подобия треугольников ALA_{1}
и AIA'
находим, что
LA_{1}=IA'\cdot\frac{LA}{IA}=\frac{b-c}{2}\cdot\frac{a+b+c}{b+c}=\frac{(b-c)(a+b+c)}{2(b+c)},
Значит,
PA_{1}=PL+LA_{1}=
=\frac{(b-c)(b+c-a)}{2(b+c)}+\frac{(b-c)(a+b+c)}{2(b+c)}=b-c.
Тогда PA_{1}=2PM
, а значит, M
— середина отрезка PA_{1}
. Следовательно, BP=CA_{1}
, и A_{1}
— точка касания со стороной BC
вневписанной окружности треугольника ABC
(см. задачу 4805).
Аналогично для прямых BB'
и CC'
. Отсюда следует доказываемое утверждение.
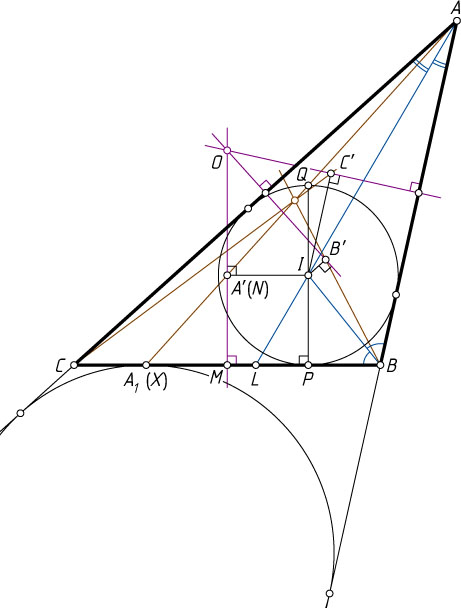
Второй способ. Пусть I
— центр вписанной окружности треугольника ABC
(рис. 2), P
— точка касания этой окружности со стороной BC
, M
— середина BC
; A_{1}
, B_{1}
и C_{1}
— точки пересечения прямых AA'
, BB'
и CC'
со сторонами BC
, AC
и AB
соответственно.
Рассмотрим гомотетию с центром A
, при которой вписанная окружность треугольника ABC
переходит во вневписанную, касающуюся стороны BC
в некоторой точке X
. Тогда CX=BP
(см. задачу 6411), MP=MX
, а прямая AX
проходит через точку Q
вписанной окружности, диаметрально противоположную точке P
(см. задачу 802).
Серединный перпендикуляр к отрезку BC
параллелен PQ
и проходит через середину отрезка PX
, значит, он пересекает отрезок QX
в его середине N
. Отрезок IN
— средняя линия прямоугольного треугольника QPX
, поэтому IN\parallel PX
. Значит, IN\perp MN
, и точка N
совпадает с проекцией точки I
на серединный перпендикуляр к стороне BC
, т. е. с точкой A'
. Тогда точка X
совпадает с точкой A_{1}
, а прямая AA'
— с прямой AA_{1}
.
Аналогично прямая BB'
совпадает с прямой BB_{1}
, прямая CC'
— с прямой CC_{1}
, а так как прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке — точке Нагеля (см. задачу 4284), то утверждение доказано.
Источник: Ефремовъ Д. Д. Новая геометрiя треугольника. — Одесса, 1902. — № 19, с. 24

