5940. Точки касания вписанной и вневписанной окружностей прямоугольного треугольника делят гипотенузу на три равных отрезка.
а) Докажите, что разность радиусов этих окружностей равна гипотенузе.
б) Найдите произведение радиусов окружностей, если гипотенуза равна 3.
Ответ. 2.
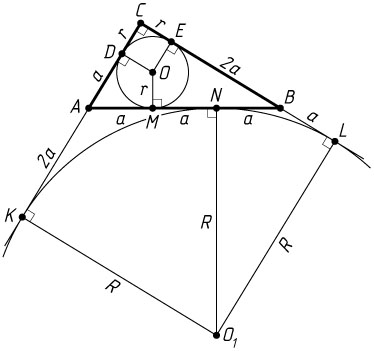
Решение. Первый способ. а) Пусть вписанная окружность радиуса r
с центром O
касается гипотенузы AB
прямоугольного треугольника ABC
в точке M
, катетов AC
и BC
— в точках D
и E
соответственно; вневписанная окружность радиуса R
с центром O_{1}
касается гипотенузы в точке N
и продолжений катетов AC
и BC
— в точках K
и L
соответственно, причём AM=MN=BN=a
. Тогда
AB=3a,~AD=AM=a,~AK=AN=2a.
Четырёхугольники CKO_{1}L
и CDOE
— квадраты, поэтому
R=O_{1}L=CK=DK+CD=AK+AD+CD=2a+a+r=3a+r.
Следовательно,
R-r=3a=AB.
б) По теореме Пифагора
AB^{2}=AC^{2}+BC^{2},~9a^{2}=(a+r)^{2}+(2a+r)^{2},~r^{2}+3ar-2a^{2}=0.
Отсюда, учитывая, что a=1
, находим, что
r=\frac{a(\sqrt{17}-3)}{2}=\frac{\sqrt{17}-3}{2}.
Тогда
R=3a+r=3+r=3+\frac{\sqrt{17}-3}{2}=\frac{\sqrt{17}+3}{2}.
Следовательно,
rR=\frac{\sqrt{17}-3}{2}\cdot\frac{\sqrt{17}+3}{2}=2.
Второй способ. а) Пусть вписанная окружность радиуса r
касается гипотенузы AB
прямоугольного треугольника ABC
в точке M
, катета AC
— в точке D
; вневписанная окружность радиуса R
с центром O_{1}
касается гипотенузы в точке N
и продолжений катетов AC
и BC
— в точках K
и L
соответственно, причём AM=MN=BN=a
, а полупериметр треугольника равен p
. Тогда
AB=3a,~R=O_{1}L=CK=p,~r=CD=p-AB=p-3a
(см. задачи 217, 219, 4805). Следовательно,
R-r=p-(p-3a)=3a=AB.
б) Пусть площадь треугольника ABC
равна S
. Тогда
r=\frac{S}{p},~R=\frac{S}{p-AB}=\frac{S}{p-3a}
(см. задачи 452, 392). Следовательно (см. задачи 2730, 219),
rR=\frac{S}{p}\cdot\frac{S}{p-3a}=\frac{S^{2}}{p(p-3a)}=\frac{p(p-3a)(p-AC)(p-BC)}{p(p-3a)}=
=(p-AC)(p-BC)=BM\cdot AM=a\cdot2a=2a^{2}=2.
Примечание. Поскольку площадь прямоугольного треугольника ABC
равна произведению BM\cdot AM
(см. задачу 4862), то площадь прямоугольного треугольника, удовлетворяющего условию AM=MN=BM
, равна произведению радиусов вписанной и наибольшей из вневписанных окружностей, т. е. S=rR
.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 11.51.2, с. 120
