10880. Пусть AA_{1}
и BB_{1}
— высоты неравнобедренного остроугольного треугольника ABC
, P
— вторая точка пересечения описанных окружностей треугольников ABC
и A_{1}B_{1}C
. Касательные, проведённые к описанной окружности треугольника ABC
в точках A
и B
, пересекают прямую A_{1}B_{1}
в точках X
и Y
соответственно и пересекаются в точке Z
. Докажите, что описанные окружности треугольников ABC
и XYZ
касаются в точке P
.
Указание. См. задачи 6401, 4785, 700, 5000, 533, 10876, 3180 и 10879.
Решение. Точка P
лежит на описанной окружности треугольника ABC
, поэтому достаточно доказать, что P
— центр гомотетии, переводящей эту окружность в описанную окружность треугольника XYZ
(см. задачу 6401).
Пусть CC_{1}
— третья высота треугольника ABC
, а H_{a}
, H_{b}
и H_{c}
— образы ортоцентра H
треугольника ABC
при симметриях относительно прямых BC
, AC
и AB
соответственно. Точки H_{a}
, H_{b}
и H_{c}
лежат на описанной окружности треугольника ABC
(см. задачу 4785). Из теоремы о средней линии треугольника следует, что при гомотетии с центром H
и коэффициентом \frac{1}{2}
треугольник H_{a}H_{b}H_{c}
переходит в треугольник A_{1}B_{1}C_{1}
, который, в свою очередь, гомотетичен треугольнику YXZ
, так как стороны этих треугольников соответственно параллельны (см. задачи 700 и 5000). Следовательно, треугольник H_{a}H_{b}H_{c}
гомотетичен треугольнику YXZ
.
При этой гомотетии, описанная окружность треугольника H_{a}H_{b}H_{c}
(т. е. описанная окружность треугольника ABC
) переходит в описанную окружность треугольника YXZ
, а так как H
и середина M
стороны AB
— центры вписанных окружностей треугольников H_{a}H_{b}H_{c}
и YXZ
соответственно (см. задачи 533 и 10876), то прямая MH
проходит через центр гомотетии. В то же время, через центр этой гомотетии проходит и прямая ZH_{c}
. Осталось заметить, что точки M
, H
и P
лежат на одной прямой (см. задачу 3180) и точки Z
, H_{c}
и P
лежат на одной прямой (см. задачу 10879). Следовательно, прямые MH
и ZH_{c}
пересекаются в точке P
, т. е. P
— центр рассматриваемой гомотетии. Что и требовалось доказать.
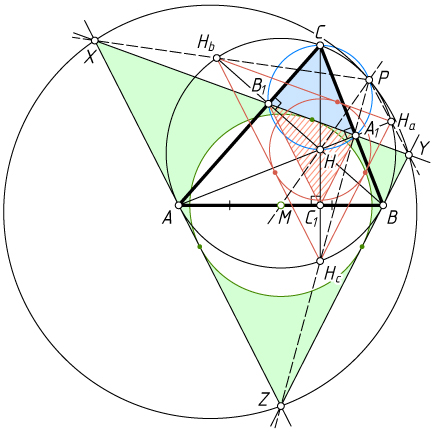
Примечание. См. статью Ю.Блинкова «Ортоцентр, середина стороны, точка пересечения касательных и ... ещё одна точка!», Квант, 2014, N1, с.43-46.
Автор: Зайцева Ю. И.
Источник: Журнал «Квант». — 2014, № 1, с. 45
